To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Rozwiązanie: x1 - ilość W1
x2 - ilość W2
f. celu: z= x1 + x2 → max ( maksymalizacja wielkości produkcji) warunki ograniczające: 6 x1 + 6x2 ≤ 36000
10x1+ 5x2 ≤ 50000
x2 ≤ 4000
warunki nieujemności: x1≥0
x2≥0
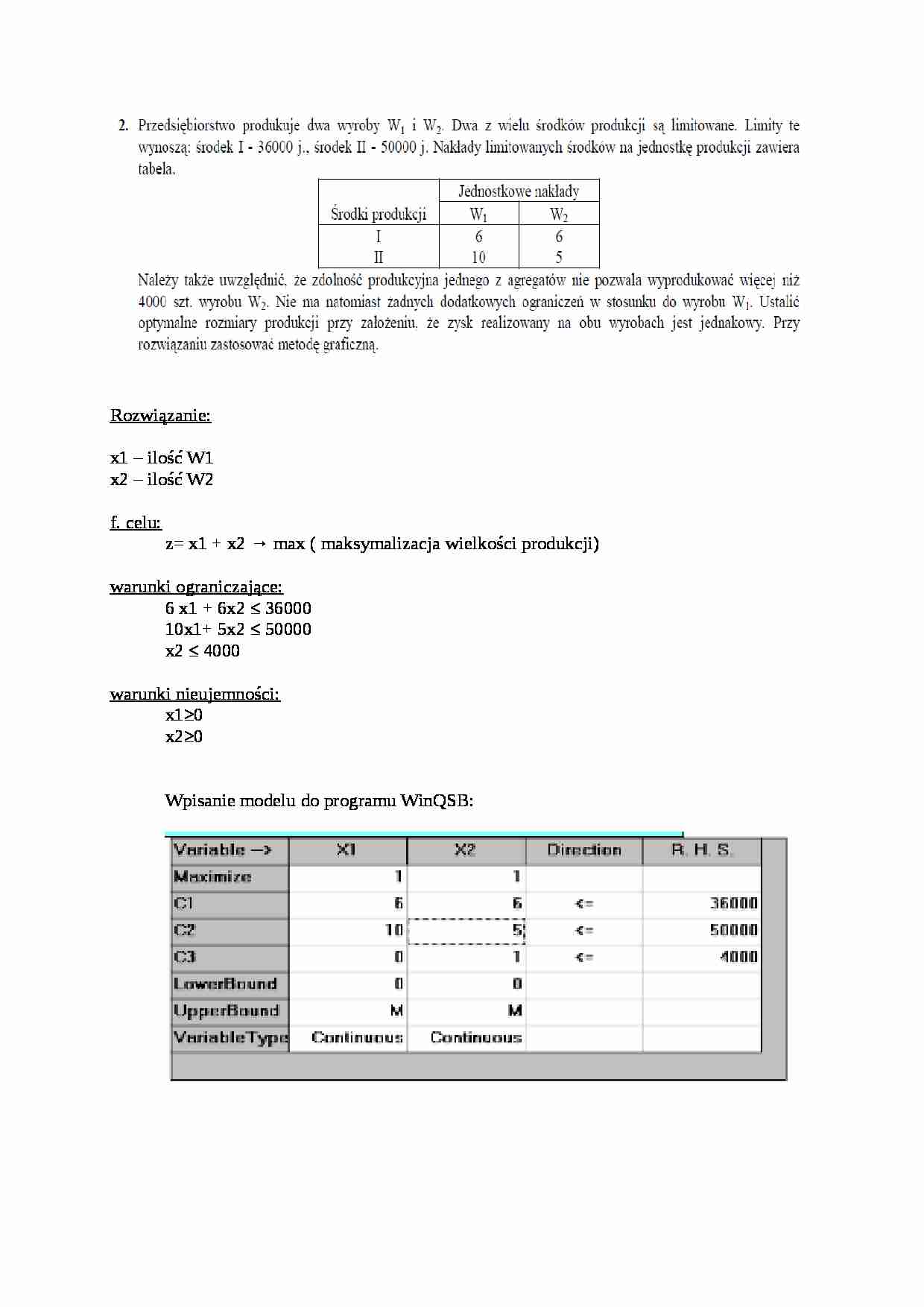
Wpisanie modelu do programu WinQSB:
Graficzne rozwiązanie:
Funkcja celu ma nieskończenie wiele rozwiązań.
Optymalna wielkość produkcji wynosi, 6000 przy czym ilość w1 wynosi 4000 a w2 2000.
Tablica wynikowa:
Maksymalna wartość funkcji celu wynosi 6000
Optymalna wartość zmiennej decyzyjnej x1 = 4000
Optymalna wartość zmiennej decyzyjnej x2 = 2000
Aby osiągnąć optymalne rozmiary produkcji należy produkować 4000j. wyrobu w1 oraz 2000 j. wyrobu w2. Występuje alternatywne rozwiązanie. W rozpatrywanym przykładzie wszystkie koszty względne są równe zero, gdyż optymalne wartości zmiennych decyzyjnych są dodatnie. Optymalne zakresy współczynników funkcji celu c1 i c2 związanych odpowiednio ze zmiennymi x1 i x2 są następujące:
1≤ c1 ≥ 2
0,5 ≤ c2 ≥ 1
Dla jednostkowego zysku z wyrobu 2 nie większego od 1 i nie mniejszego 0, 5 i dla jednostkowego zysku z wyrobu 1 nie większego od 2 i nie mniejszego niż 1, zawsze otrzymamy rozwiązanie optymalne problemu wyznaczone przez punkt (4000,2000)
Jedynie dla ograniczenia x2 ≤ 4000 lewa strona ograniczenia nie jest równa prawej stronie ograniczenia. Reszta wynosi 2, a zatem występuje nadmiar, oznacza to iż limit wyrobu drugiego (w2) nie został w pełni wykorzystany natomiast limit wyrobu pierwszego (w1) został wykorzystany w pełni. Wielkości cen dualnych: jeśli prawą stronę ograniczenia 6 x1 + 6x2 ≤ 36000 zwiększymy o jednostkę, to maksymalny zysk całkowity z produkcji nowych wyrobów wzrośnie o 0,1667. Wartość zerowa ceny dualnej dla pozostałych ograniczeń wskazuje, że żadna zmiana wartości prawej strony tych ograniczeń nie zmieni optymalnej wartości funkcji celu.
Zwiększenie prawej strony ograniczenia, 6 x1 + 6x2 ≤ 36000, z 36000 do 37000 (o 1000 jednostek) spowoduje wzrost optymalnej wartości funkcji celu o 166,7, oznacza to, że gdyby przedsiębiorstwo produkowało o 1000 jednostek więcej to zarobiłoby o 166,7 zł więcej. Dalsze zwiększanie wartości prawej strony ograniczenia spowoduje wzrost optymalnej wartości funkcji celu pod warunkiem, że prawa strona ograniczenia wyniesie maksymalnie 42000. Natomiast zmiana wielkości produkcji w przypadku pozostałych ograniczeń nie wpływa na zmianę optymalnej wartości funkcji celu.
... zobacz całą notatkę






Komentarze użytkowników (0)